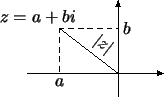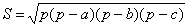Комплексное число можно представить в виде a+bi, где a – реальная, b – мнимая часть числа, а i – мнимая единица (
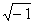
).
Совет
Модуль комплексного числа z представляет собой корень квадратный из суммы квадратов реальной и мнимой частей, а аргумент комплексного числа представляет собой арктангенс отношения мнимой части к реальной части:
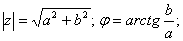
Внимание
При a=0 аргумент не может быть определен.
"Квадратным" называется уравнение вида
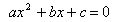
при a<>0.
Корни квадратного уравнения производится по формуле
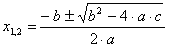
. Выражение
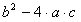
называется дискриминантом.
Внимание
При отрицательном дискриминанте (когда
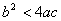
) уравнение не имеет корней в действительной области, только комплексные.